在N边形内任取一点,和各个顶点相连,就构成了N个三角形,它们的内角各就是180N;再减去中心一个圆周角的度数就行了。
设多边形的边数为n,从它的一个顶点出发引对对角线,除了这点本身、和与它相邻的两个顶点外,与其他的顶点所连接的线段都是对角线,故这样的对角线可引 (n-3)条;n边形有n个顶点,所以可以引 n(n-3)条。
又因为n(n-3)条中每条对角线都计算了两次,凸多边形的对角线共有:n(n-3)/2 条,所以凸多边形的对角线公式是n(n-3)/2 条。
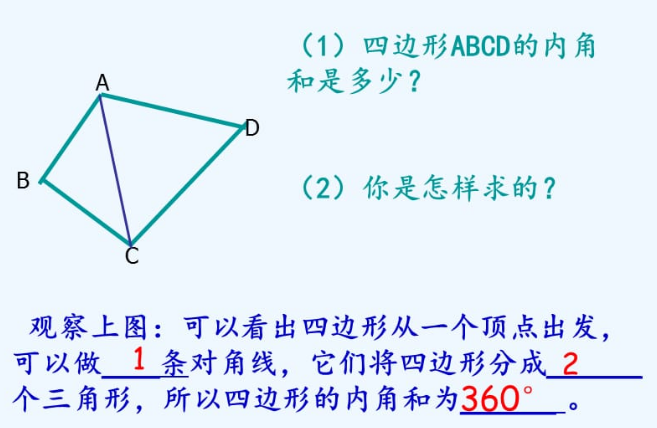
由三条或三条以上的线段首尾顺次连接所组成的平面图形叫做多边形。按照不同的标准,多边形可以分为正多边形和非正多边形、凸多边形及凹多边形等。
在平面多边形中,边数相等的凸多边形和凹多边形内角和相等。但是空间多边形不适用。可逆用:
n边形的边=(内角和÷180°)+2。
过n边形一个顶点有(n-3)条对角线。
n边形共有n×(n-3)÷2=对角线。
n边形过一个顶点引出所有对角线后,把多边形分成n-2个三角形。
推论:
(1)任意凸形多边形的外角和都等于360°。
(2)多边形对角线的计算公式:n边形的对角线条数等于1/2·n(n-3)。
(3)在平面内,各边相等,各内角也都相等的多边形叫做正多边形。【两个条件必须同时满足】
反例:矩形(各内角相等,各边不一定相等);菱形(各边相等,各内角不一定相等)。